
Video: Hvad er summen af koefficienterne i en række i Pascals trekant?
2024 Forfatter: Edward Hancock | [email protected]. Sidst ændret: 2023-12-16 01:30
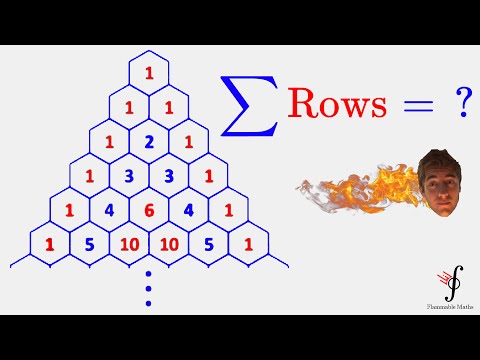
Sætning. Det sum af alle poster i n'et række af Pascals trekant er lig med 2n.
På samme måde kan man spørge, hvordan kan du finde koefficienterne for enhver række af Pascals trekant?
Bestemmelse koefficienter med Pascals trekant . Hver række giver koefficienter til (a + b) , begyndende med n = 0. For at finde binomialet koefficienter for (a + b) , brug den n'te række og start altid med begyndelsen. For eksempel binomialet koefficienter for (a + b)5 er 1, 5, 10, 10, 5 og 1 - i nævnte rækkefølge.
Og hvad er formlen for Pascals trekant? EN Formel for enhver indgang i The Trekant Notation: "n vælg k" kan også skrives C(n, k), Ck eller endda Ck. Det "!" er "faktoriel" og betyder at gange en række faldende naturlige tal. Eksempler: 4! = 4 × 3 × 2 × 1 = 24.
I overensstemmelse hermed, hvad er den n'te række i Pascals trekant?
Den n'te række af Pascals trekant er: (n−10) (n−11) (n−12) (n−1n−1) Det vil sige: (n−1)!
Hvad er Pascal formel?
I matematik, Pascals regel (eller Pascals formel ) er en kombinatorisk identitet om binomiale koefficienter. Den siger, at for positive naturlige tal n og k, hvor. er en binomial koefficient; en fortolkning af dette er koefficienten af xk led i udvidelsen af (1 + x).
Anbefalede:
Hvad betyder det universelle kald til hellighed, og hvad kræver det af os?

Det universelle kald til hellighed er at følge Jesu vej, kærlighedens vej uden mål, som medlemmer af kirken. Den beder os om at bidrage til opbygningen af kirken, gøre kirken mere kærlig, mere medfølende og fylde den med mere glæde og godhed
Hvad er accept Hvad er accept?

Et tilbud er et åbent opkald til alle, der ønsker at acceptere tilbudsgiverens løfte og bruges generelt til produkter og tjenester. Accept sker, når en tilbudsmodtager indvilliger i at være gensidigt bundet til vilkårene i kontrakten ved at give vederlag eller noget af værdi som penge for at forsegle handlen
Hvordan bruges Pascals trekant i algebra?

Pascals Trekant er en aritmetisk trekant, du kan bruge til nogle pæne ting i matematik. Når folk taler om en post i Pascals trekant, giver de normalt et rækkenummer og en plads i den række, begyndende med række nul og plads nul. For eksempel vises tallet 20 i række 6, plads 3
Hvad var den anden store opvågning, og hvad var dens virkninger?

Den anden store opvågning havde en dyb indvirkning på amerikansk religiøs historie. Baptisternes og metodisternes numeriske styrke steg i forhold til den for de trosretninger, der dominerede i kolonitiden, såsom anglikanerne, presbyterianerne, kongregationalister og reformerte
Hvad spørger ikke hvad dit land kan gøre for dig spørger hvad du kan gøre for dit land?

Det var også i sin tiltrædelsestale, at John F. Kennedy talte sine berømte ord: 'Spørg ikke, hvad dit land kan gøre for dig, spørg, hvad du kan gøre for dit land.' Denne brug af chiasmus kan endda ses som en afhandling af hans tale - en opfordring til handling til offentligheden om at gøre det rigtige for det større gode
